 When developing vehicle physics the tire is the single component that has the most influence in the entire system. When designing a tire simulation the Pacejka Curves arise sooner or later.
When developing vehicle physics the tire is the single component that has the most influence in the entire system. When designing a tire simulation the Pacejka Curves arise sooner or later.
What’s “Pacejka” exactly?
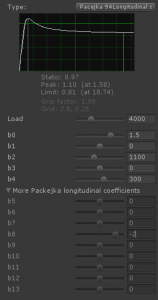
First of all, the Pacejka Magic formula, also called simply Magic Formula “MF” or “MF-tyre”, is a function y=f(x) which is used to predict and simulate the forces developed by a tire. Given an input x and a list of coefficients (b0..b12 in the picture), the function calculates the force y developed by the tire. Three different functions are used, one for longitudinal forces, other for lateral forces, and the last one for the self-aligning torque (the feedback force you experiment on your car’s steering wheel). Each function has its own set of coefficients.
The coefficients affect the final shape of the curve in a wide variety of ways (see the pic). The goal is fitting the curve with the results obtained in the empiric experiments on the specific tire the curve is being calculated for. Once the proper coefficients for the curve are found, the behavior of that tire can be easy and realistically predicted without having to actually use the real tire. One can imagine using a tire testing facility, testing a specific tire in a wide variety of conditions and measuring the results. Then, based on those results, one could start toying with the coefficients of the Pacekja curves until getting a curve that acceptably fits the experimental results.
What about the coefficient sets for Pacejka curves?
Pacejka and other models are developed by and for the automotive industry. Real coefficient sets are scarce and hard to find, as they are heavily protected intellectual data. Tire manufacturers sell the coefficient sets to interested customers who can then simulate how a specific tire would behave in a vehicle (the MSC Adams software is an industry-standard for modelling this kind of simulations). A Pacejka coefficient set for a single tire model can easily cost around $1000-1500.
You may find many Pacejka sets over there (for instance as part of the car add-ons for the Racer.nl simulator). But most of them are not real Pacejka sets as they haven’t been calculated based on measures on the real tires. Anyone can use a Pacejka editor and get an arbitrary set of coefficients. For that, the Pacejka formula is a realistic and flexible method for simulating an imaginary tire based on the behavior expected in a simulated vehicle.
I’ve written a document which describes how each Pacejka coefficient affects the resulting curve. This is useful for designing tire friction curves matching a specific behavior in vehicle simulation games.
Is Pacejka a necessary or best method for simulating tires?
Surprisingly, the curves themselves are not the most important part of a tire simulation. Remember, a Pacejka curve is simply a function y=f(x). Any function with shape similar to Pacejka (peak – asymptote) will work, no matter how it’s calculated. It could result more or less realistic, but even just a flat, clamped slope will do a decent work.
The critical part for simulating a tire is how are you calculating the parameters you will feed the curves with. The “x” in y=f(x). And here, my friend, is where things get serious.
What are the problems with the Pacejka-based methods?
Pacejka and other models are based on the amount of slip of the tire over the ground. The longitudinal version uses the difference between the tire’s angular velocity and the actual velocity over the ground (slip ratio). The lateral version is based on the angle between the wheel’s heading direction and the true movement direction (slip angle).
However the slip ratio is a tricky concept. Having slip doesn’t mean that the tire is actually sliding over the ground. The slip ratio reflects the fact that the drive wheels compress the tire at the front of the contact patch where the radius of the wheel is smaller, so it effectively travels faster than the ground underneath. A portion of the contact patch is adherent to the surface while the other portion is slipping. This slip ratio generates the force that moves the car. In a car cruising at constant speed the drive wheels will be spinning a bit faster than the non-drive wheels.
There are several different definitions for slip ratio and slip angle available. These ones are a commonly used definition borrowed from the great book from Brian Beckman The Physics Of Racing:
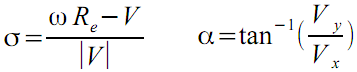
ω angular velocity
Re effective radius
V lineal velocity
Vy lateral velocity
Vx longitudinal velocity
The slip ratio σ and slip angle α are the input for the Pacejka formulas, which yield the longitudinal and lateral forces exerted by the tire. Although this kind of methods is known to provide the state-of-the-art tire simulation, they still exhibit severe problems:
- A quick look at the formulas reveal an evident and inconvenient fact: the slip formulas become numerically unstable when V approaches zero and are not defined at all when the vehicle is stopped (0/0). Other definitions of the slip ratio also suffer of this problem in a similar way, requiring hacks and workarounds at low speeds.
- The lateral force is based on the slip angle. However the slip angle does not account for any variation with the speed. Intuitively, the forces generated at high speed must be greater than the forces at low speed with the same slip angles. But using these formulas a velocity of V = (0.2, 0.1) = 0.22 m/s, results in the same slip angle (and thus the same lateral force) as V = (20, 10) = 22.36 m/s.
Is there a better method?
Of course, there are always better methods. The challenge here is to design a method that is fully coherent yet realistic enough that works under all conditions of the tire, including the forces at low speeds and with the vehicle stopped.
This is what I’m currently working on 😉
EDIT (March 2015):
…and finally I’ve designed and implemented a fully coherent and accurate tire model and vehicle simulation that resolves all issues mentioned in this article. The tire and vehicle simulation react realistically to all situations with perfect continuity between all states.
https://www.edy.es/dev/2014/11/early-preview-of-vehicle-physics-pro/
fantastic work man. much of the math is over my head but damn interesting none the less.
have you experimented at all with getting force feedback into the mix?
http://forum.unity3d.com/threads/78268-Force-feedback-for-Windows?p=501186#post501186
I’ve been playing a lot of Project CARS lately. Damn realistic tire physics are addicting 🙂
I never got into rFactor, iRacing, netKar pro or any others from the last gen of sim racing, but i’m damn stoked for the immanent beta of rFactor 2. Check out this vid showcasing their new tire model: http://www.youtube.com/watch?v=PG0lscEUqBk
Thanks!
Yes, I already have a clear idea on how to calculate the force feedback from the tire (a.k.a. self aligning torque) without having to deal with artificially calculated curves.
Addicting, you tell me? 😀
Nice rFactor video!
Very nice to see your knowledge on the subject has expanded significantly since the last time I looked into all of this.
I trust you looked into Brian Beckmans simplified alternative formula? In fact are you still using slip curves at all?
Of course I’m using slip curves. They are what define a tire’s handling and behavior. Actually I’ve implemented parametric curves (where you specify the peak and asymptote points directly) as well as Pacekja’94 longitudinal and lateral curves. In fact, the picture for this article reveals my Pacejka editor for Unity 3D 😉 it allows to edit the curve and see the results directly on both the graph and the vehicle’s behavior.
As said, the curves themselves are not the most important part of a tire model: it’s the way you “feed” them. My tire model allows to use the curves properly even when the vehicle is completely stopped. For instance, the tires generate force based on their slip curves when the vehicle is parked on a slope, so it remains static.
I looked at the Beckmann’s simplified formula. It’s visually simpler but more difficult to configure. Its three parameters are inter-related so if you want, for instance, modify the peak (point of maximum grip) you have to adjust all three parameters in a pure trial & error way. On the other hand, the Pacejka parameters are clearly defined and each one has a specific, predictable effect on the curve. Anyways it would be easy to add the simplified formula to the available options.
About Pacejka coefficient sets, your information here is a bit missleading. There simply is no sets sold. The reason why there arent many sets is because, there simpy is no actual sets. Because, while measuring tires, they get destroyed, every little measurement destroys rubber. There are good pacejkas but no 1:1 copy. Mostly they are behind logical thinking of a tire designer & a physicist & some new and better and advanced technology.
This is mainly the reason why pacejka coeficient sets are rear AND always free (so dont buy any pacejka sets if someone try’s to sell you some, it’s a scam)
Also i didn’t notice if you covered the friction combining part, thats the one and most important part of a tire model giving you realistic feedback. Without it your tires will allways feel wrong no matter how good your coeficient sets (friction curves) are.
Try searching for brian beckmans combining method (the unity3d alternative car tutorial actually has it, but in a little different form) Hope this helps someone!
According to the information available I must disagree.
Tire manufacturers like Michelin offer true Pacejka sets for their tire models through their Engineering & Services division (LINK).
Here you can read a discussion (
LINK) by several representatives of car design teams about getting real experimental data from tires. One of them gets quoted more than $3000 for two basic tests and data acquisition on a tire testing facility.That data is the same kind of experimental data the Pacejka coefficients are calculated from. The book Tratado Sobre Automóviles Vol. 4 (LINK) (in spanish) describes in a detailed and comprehensive way how the real data retrieved at experimental tests with the tire are used to build the Pacejka coefficients for that tire (LINK to a preview of the relevant pages, in spanish).
In addition I read somewhere (can’t recall the exact page) about a teacher asking a tire manufacturer for a Pacejka set for educational purposes and being quoted about $1600. This is the example price used in my article.
Sure, I’ve read Beckman’s book and in fact I’m using his combining method in my own tire friction model. But this is a second stage, and it’s easily applicable once you have the longitudinal and lateral friction models working properly. If longitudinal-lateral forces are not properly defined, the combination method won’t likely improve anything.
UPDATE: I’ve found this really interesting page (LINK) describing how a real set of coefficients are calculated out of the raw data gathered using a tire stability rig. At the bottom of the page it shows a real set of coefficients for the Magic Formula. Other page describes a different method (LINK) for getting more precise results.
Yeah I was wrong, there are real pacejka sheets, but what I actually ment was that combining these foreces (what you need to do for game/simulation use) you will loose alot of data, and since the former models are old (1989, 1994) they have alot of downsides when it comes to realism. One of the most common issue on todays sims are wheelspin. Anyway I still use pacejka 89, because its easy and quick to setup, trying to figure out some solutions to eliminate the errors (witch i will probbably fail, because i’m not the first one who trys this)
Hi Edy
I would like to know how to measure the force feedback from the tire….?Could you please help me explaining it…
Thanks…
Hi,EDY
Do you know Ftire model? It is another tire model which is more accurate than Pacejka, especially in high frequency.
Do you know clearly the parameters in Ftire model?
If yes, could you please help me to understand it?
lcy111989@gmail.com this is my email~
Thanks!
Hi Edy,
Thank you for linking to my site. If you want to receive some real racing tyre data or to talk about a more appropriate model than the MF-Tyre(Pacejka)for you purposes, then contact me direct.
Best regards, White-Smoke
Interesting editor.
Btw the Beckmann’s simplified formula is as good as any of the Pacejka variations, unless you run your engine on a super-computer at an insane rate. I adapted it in my engine (under development) so you don’t have to use trial and errors, and made a new formula for the self aligning torque.
But here is a lot of snobism in general about realism in games.
First any curve other than pacejka would work as long as the model is including combinaison slip and grip. An empirical (semi?) is as good as another. A pacejka model doesn’t deal very well with tire flex I suppose.
Second, to get as near as possible to realism (without never reaching it), there are a lot of things to simulate beyond the tire model itself : chassis flex, rolling moments, proper differentials (lsd etc.. they are essential for the behaviour).
Then any tire model based on a curve such as Pacejka will only work good on tarmac. Offroad behaviours (gravel, dirt, snow etc…) requires completely different tire models.
I suppose Pacejka curves are an amazing discovery, and definitely a good tool, but when running a game at 60Hz they are completely overrated and often used in isolation of many other systems which are as important for the behaviour of the vehicle.
I think a game which could be qualified of “realistic” would be Richard Burns rally. No idea how they did their tire model but it definitively feels near a real driving experience.
In summary i think it’s kind of weird to use a as “realistic” as possible tire model, when other systems aren’t pushed that far and that we race with a keyboard on a simulation running at 60Hz.
My 2 cents!
best
@Pierre …or you can define a simplified model and ensure that your design and implementation is physically realistic and fully coherent withing the bounds of that model. In simulation we are always using models or “simplifications” of the reality. One can define how much “reality” the model should span.
In Vehicle Physics Pro the simulation model is a simplification where the reactions of tires and vehicles are relatively easy to simulate yet providing fully accurate and physically realistic results (bound to the limits of the simplified model). Check out this early preview video.
Hi Edy,
I understand the separate forces that Pacejka generates, my question specifically would be though: how do you combine them? I doubt it’s a simple Fx + Fy story, or am I wrong in thinking it’s more difficult than that?
I’m not aiming for realism, it’s why I stepped away from using the full Pacejka code from either your page/the Unity 3.0 tutorial, and went with the load-independent formula you posted as well, the simplified version. However that still doesn’t cover combining the forces and I’m kinda stumped on that honestly.
If you could give some insight, it’d be mighty appreciated
@Emily Brian Beckman’s free book “The Physics Of Racing” describes a combination method in the chapters 24 and 25. This method should be taken carefully though. It works fine at the boundaries of the reference used, the peak forces in this case. That’s the picture at the end of chapter 25. But the method produces artifacts in the outer boundaries of the curve. Those would be appreciated in a zoomed-out version of the picture in chapter 25. Anyways, it’s a good starting point for learning how a tire force combination method works and its requirements.
Note that using Pacejka doesn’t necessarily mean the results will be more realistic, as I described in the article. Not even the full formula. The demos of Vehicle Physics Pro I’ll be posting today don’t use Pacejka curves for the tire configuration but a parametric curve defined by a few direct parameters. The results are pretty realistic, as you can try yourself. Pacejka would be useful when simulating a specific commercial tire we have a proper Pacejka set for. Otherwise you are doing an educated trial & error, and it’s much easier to do that with direct parameters.
@Edy thanks for your response, unfortunately with Brian Beckman’s book I can’t get further. Math is easy for me when I understand it, but incredibly difficult for me when I don’t understand it, and it seems like a lot of information online comes with the prerequisite that you should already know what all the symbols mean and such without any examples (like, if we put in these values to this equation, this is the result)
I’ve been trying to get simple arcade physics like NFS Underground 2 for instance working for years now, and I am understanding more and more slowly but it’s going super slow and I have a very hard time finding information when I need it. (It took me 3 weeks to find out how to calculate ackermann steering angles lmao)
So I appreciate your comment but it doesn’t really help me much unfortunately. I’ll just keep trying I guess ^^;
@Emily Well, math is a necessary prerequisite. I’m not particularly good at math either, but I’ve managed to understand the Beckman’s combination method in a way to implement it first, and improve it later. Note that the Part 25 of the book is exactly what you say: it puts actual values into the equations, then shows the results as graphs.
Learning to use math tools like Wolfram Mathematica is also a plus, as it can do all the plumbing for you (i.e. solve a variable in an analytical equation defined just by letters, without actual numbers).
It took me three years to figure out, design and implement the coherent wheel and tire model in Vehicle Physics Pro. This is not an easy topic, so don’t be discouraged if it takes time.